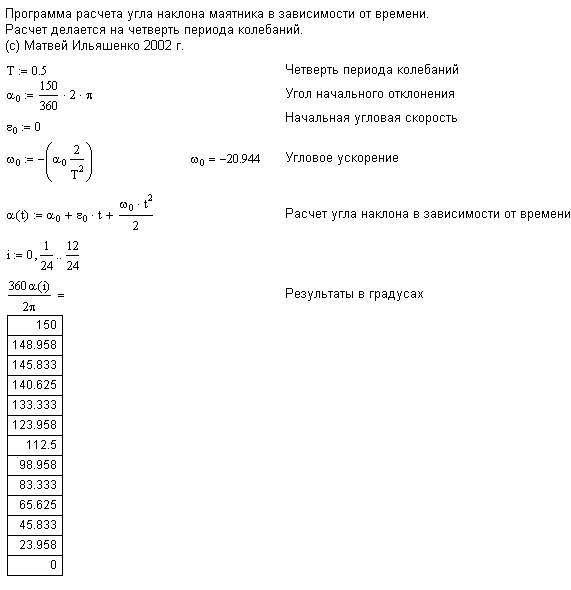Правильно колеблющийся маятник. На этой страничке: Описание примера
Download (Скачивание) 
Начало страницы
Описание примера. Понемногу окунаясь в мир 3D я часто встречал различные маятники и периодически колеблющиеся предметы. Да вот беда, все они качались неправильно.
Аниматоры шли по пути наименьшего сопротивления. В какой-то момент времени задавалось начальное отклонение маятника от положения равновесия, откручивалось несколько кадров, выставлялось конечное отклонение. Аналогично делалался и обратный ход маятника.
На самом деле, еще в курсе физики 9-го класса рассказывается, как работает маятник. В положении максимального отклонения от равновесного, вся энергия колебаний маятника сосредоточена в потенциальной. В процессе колебаний энергия переходит в кинетическую и обратно в потенциальную. При этом, на маятник действует ускорение свободного падения, которое заставляет его качаться с неравномерной угловой скоростью.
Приведу несколько простейших формул:  | период колебаний
l - длина маятника от оси вращения до центра масс
g - ускорение свободного падения =9.8 H/м | 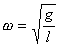 | угловое ускорение
l - длина маятника от оси вращения до центра масс
g - ускорение свободного падения =9.8 H/м | | | Из вышенапечатанного следует, что если период колебаний маятника - T, то с учетом углового ускорения можно расчитать угол наклона маятника в каждый момент времени (в момент каждого кадра в нашем случае). Эти действия реализует следующая программа для MathCad: 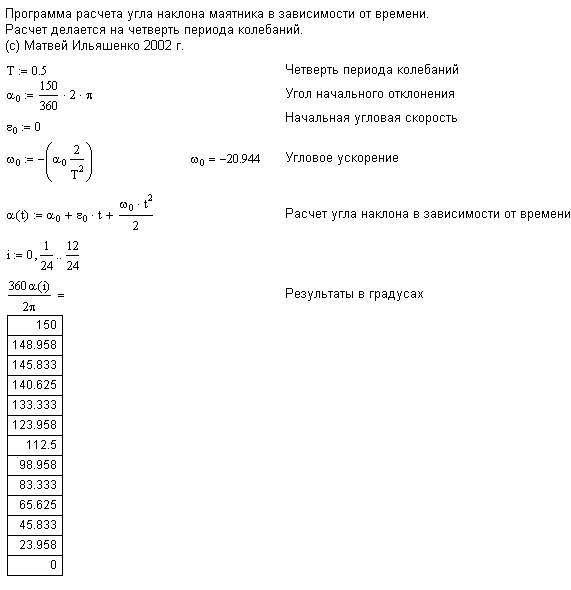
Все использованные формулы известны из школьного курса физики. На начальном этапе углы наклона маятника можна ввести и вручную. В более сложной сцене можно написать малюсенький скриптик или скопировать отдельно созданный маятник вместе с ключами анимации.
В программе расчитаны углы только для четверти периода исходя из предпосылки, что анимация делается в формате с 24-мя кадрами в секунду. Для первых 12-ти кадров углы приведены, для следующих 12-ти те же углы следуют в обратном порядке и с отрицательным знаком. Так формируется первая секунда. Вторая секунда полностью повторяет первую, но кадры следуют в обратном порядке, и параметры модели для каждого кадра выставляются равными параметрам на соответствующем кадре первой секунды.
Далеко не маловажно то, что сцена анимируется с расчетом на автоповтор клипа при просмотре (т.е. при автоповторе первый кадр согласуется с последним и служит его продолжением). Как видно из результатов работы программы, на 11-м кадре угол наклона маятника не 0, а 23.958. Соответственно на 47-м кадре угол наклона будет не 150, а 148.958. Этим достигается реалистичность при зацикленном просмотре клипа. Дело в том, что если на последнем кадре угол наклона маятника будет равен углу на первом кадре, то при автоповторе, в момент "склейки" последнего и первого кадра получится, что одно изображение повторяется дважды поряд, что пагубно сказывается на реалистичности.
Если углы наклона маятника на последнем и первом кадре равны, то из этого следует, что период его колебаний составит не 2 секунды, а чуть меньше - 47/24 секунды, т.к. последний кадр клипа уже будет относиться к следующему периоду колебаний. Если зациклить такой маятник, то очень быстро он не будет колебаться синхронно с часами. и если в первом случае модель можно использовать, скажем, в качестве заставки ждущего режима, которая будет не только показывать время, но и отсчитывать его с помощью маятника, то во втором случае такого не получится.
Надеюсь, что несколько научное изложение материала читателя не отпугнуло. Просто я люблю, чтобы все было продуманно и реалистично. Более интересной будет наверное демонстрация результатов напряжения стольких извилин мозга: |